DSC（示差走査熱量計）によるタンパク質の熱安定性評価（3）

大阪大学大学院工学研究科生命先端工学専攻
内山　進

• DSC（示差走査熱量計）によるタンパク質の熱安定性評価（1）はこちら
• DSC（示差走査熱量計）によるタンパク質の熱安定性評価（2）はこちら

9. 会合体の熱変性の解析

タンパク質は自己会合し、2量体や3量体といったホモ会合体を形成する場合があります。こうした自己会合体が熱変性する場合には以下の3つの変性モデルが考えられます。ここでは3量体を形成する場合について例示します。

モデル1　　N3 ↔ 3D
モデル2　　N3 ↔ I3 ↔ 3D
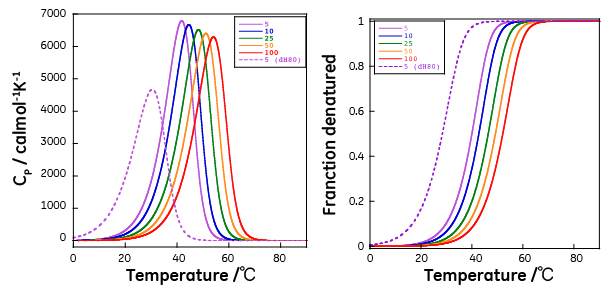
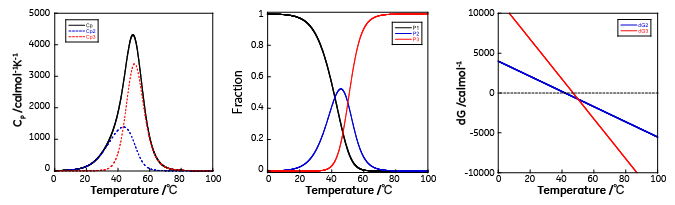
モデル3　　N3 ↔ D3

モデル1では温度上昇により解離を伴いながら天然状態（N）から変性状態（D）へと移ります。モデル2は温度上昇に伴い中間状態（I）へと移り、その後に変性状態（D）へと移るケースであり、中間状態（I）では三量体間の相互作用が維持され、変性状態へ移りはじめて3量体から単量体への解離が起きます。モデル3は3量体が共有結合で相互作用しており、変性しても分子数が変わらないケースに相当し、通常の2状態転移と同じ扱いとなります。
特異的な会合体を形成するタンパク質の熱変性はモデル1となることが多く、特に単量体の分子量が小さい場合にはこの傾向が強くなります。このように中間状態を経ずに熱変性する理由は、会合体中の単量体は単量体間の相互作用により安定化されているためです。つまり、温度上昇に伴って解離が起こり各単量体間の相互作用が消失すると、その温度では不安定である各単量体は一気に変性状態へと移ることになります。ここで、単量体間の相互作用が無いときに単量体が持つ安定性をIntrinsic stabilityといいます。ただし、変異導入により会合体間の相互作用が消失した場合でも、Intrinsic stabilityが正の値となる温度であれば変異体は不安定ながら単量体の状態で存在できます。つまり、天然型から構成された会合体はモデル1に従って中間状態を経ずに単量体へと熱変性するタンパク質でも、アミノ酸置換により単量体となる変異体は、温度によっては天然状態の単量体として存在可能であり、従って“解離＝変性”ではない点には注意する必要があります。

モデル1の場合について、数式を用いて具体的に記述します。
天然（N）状態と変性（D）状態の間の平衡定数（KND、ここではKとする）は

K = [D]3/[N3]

であり、測定に用いた試料の総濃度Ctを単量体濃度で表記すると、

Ct = 3[N3]+[D]

であり、天然状態と変性状態の比率（FNとFD）はそれぞれ以下の通りに記述できます。

FN = 3[N3]/ Ct

FD = [D]/ Ct

以上の式から以下の関係式を得ることができます。

FD3 + KFD/3Ct2-K/3Ct2 = 0

この三次方程式をFDについて解くと

FD = f（Ct, K）

を得ることができます。
変性状態と天然状態の間の自由エネルギー差(ΔGND、ここではΔGと記載)と平衡定数（KND）の間には以下の関係があります。

K　= Exp（-ΔG/RT）

さらに各温度でのΔGは変性に伴うエンタルピー変化（ΔH）、エントロピー変化（ΔS）、熱容量変化（ΔCP）、および転移温度（T0、ΔGが0になる温度）を用いて以下で表されます。

ΔG（T） = ΔH（T0）+ ΔCP（T-T0）- T（ΔS（T0）+ ΔCPLn（T/T0））

従って、

FD = f（Ct, ΔH（T0）, ΔS（T0）, ΔCP, T0, T）

と記述できます。DSCで観測されるのは、各温度における天然状態から変性状態に伴う熱容量（CP）であるため、以下の関係が成立します。

CP（T）=ΔH（T）（∂FD/∂T）=（ΔH（T0）+ ΔCP（T- T0））（∂FD/∂T）

となります。従って、ある濃度Ctの溶液についてDSCにより得たCPを非線形フィッティングにより解析することでΔH（T0）, ΔCP, T0を得ることができます。図7にT0（ΔG=0となる温度）が370K（96.85℃）、ΔH（T0）が100 kcal/mol、ΔCPが0、の場合の各濃度における熱容量、変性状態にある種の存在率の温度依存性、およびΔGの温度依存性をシミュレーションにより作成したグラフを示します。なお、濃度Ctは単量体換算した場合の総濃度（μM）です。

図7 タンパク質濃度に依存した会合体の熱容量の温度依存性（左）と変性分子の量比変化（右）

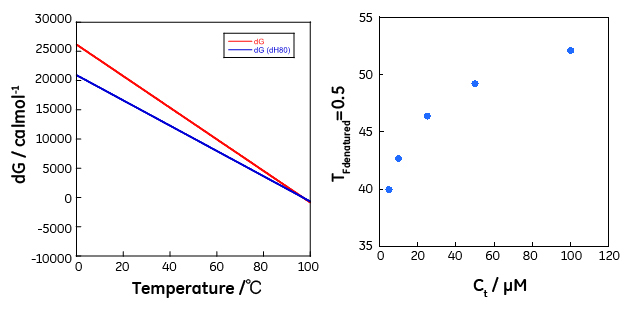
図7からも明らかなように、会合体の熱変性は、DSCにより観測されるCpが濃度依存を示すという特徴を持ちます。また、変性率の温度依存のグラフに示したように、変性率をモニター可能な分光学的手法を用いた場合にも、濃度依存を示します。これは天然状態と変性状態の間には平衡関係があり、かつ熱変性（熱転移）に伴ってモル数が変化するためルシャトリエの法則が働くことが理由です。これはCPを記述する式中に濃度Ctが入ることから理解できます。このため、変性率が0.5となる温度は図8に示したような濃度依存性を示します。解離会合系の熱転移においては以下の点にも注意を払う必要があります。変性に伴う熱力学量、ΔG、ΔH、ΔS、ΔCP、T0は濃度にかかわらず一定の値です（図7）が、転移の際のΔHが異なると、たとえ、T0が同一で濃度が同一であっても、温度に対する変性率依存性が異なります（図8）（図7中の5μMの実線と点線、T0も濃度も同一であるが観測される熱容量曲線も変性率曲線も異なります）。

図8 異なるΔHをもつタンパク質の自由エネルギーの温度依存性（左）と、変性率が0.5となる際の温度と濃度の関係（右）

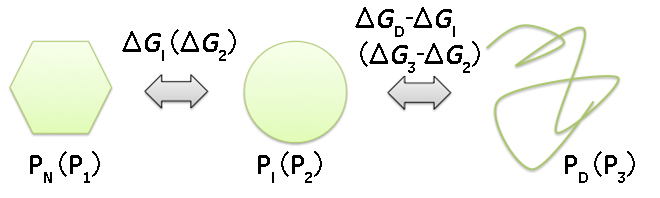
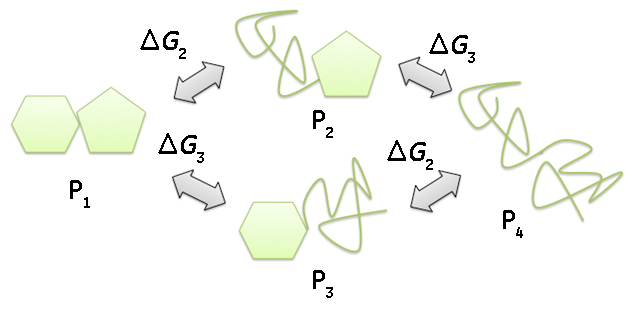
10. 中間状態を経由する熱変性の解析

マルチドメイン構造から構成されるタンパク質は、しばしば熱変性の際に中間状態を経由します。また、構造上は1種類のドメインから構成されていても、熱変性過程においては中間状態を経由する場合もあります。ここでは2種類の熱変性モデルについて説明します。

モデル4	N ↔ I ↔ D
モデル5	NAB	↔ IA’B ↔ DA’B’
		↔ IAB’ ↔

モデル4では天然状態（N）を基準状態とすると中間状態（I）の存在率をPI、変性状態（D）の存在率をPDとすると、観測される熱容量と熱力学量の関係は以下の通りになります。

P1 = exp（-ΔGI/RT）/ {1+exp（-ΔGI/RT）+exp（-ΔGU/RT）}

PU = exp（-ΔGU/RT）/ {1+exp（ΔGI/RT）+exp（-ΔGU/RT）}

天然状態の存在率PNは

PN = 1-(PI+PD)

であり、

H（T）=PIΔHI+PUΔHU
CP（T）=dH（T）/dT

であるため、

CP（T）= f（ΔHI（T0,NI）, ΔHU（T0,IU）,ΔCP,NI, ΔCP,IU,T0,NI,T0,IU,T)

と記述できます。ここで、ΔHI（T0,NI）はN状態からI状態への転移温度、T0,NI、におけるN状態からI状態への転移に伴うエンタルピー変化、ΔHI（T0,IU）はI状態からU状態への転移温度、T0,IU、におけるI状態からU状態への転移に伴うエンタルピー変化、ΔCP,NI,およびΔCP,IUは、それぞれN状態からI状態およびI状態からU状態への転移に伴う熱容量変化を表します。この関係を用い、観測された熱容量曲線を非線形最小二乗フィッティングを行うことで、転移に伴う各熱力学量を求めることが出来ます。
図9にT0,NIとT0,IUが27℃と47℃、ΔHI（T0,NI）とΔHU（T0,IU）が30 kcal/molと80 kcal/molの場合について熱容量、I状態とU状態の比率、およびΔGIとΔGUの温度依存性を示しました。

図9 安定な中間状態を有するタンパク質の熱容量曲線（左）と天然状態、中間状態、変性状態の温度依存性（中）、自由エネルギー変化（右）

図9から明らかなように、天然状態から中間状態の転移温度と中間状態から変性状態の転移温度が離れていれば、2つの転移は分離して観測され、中間状態で存在可能な温度域が広くなり中間状態を実験的に捉えることが容易になります。例えば50℃では中間状態は変性状態よりも安定なため、中間状態が全体の約9割を占めており、60℃で両者のエネルギーが同一になり、わずかな天然状態を残し、全体のほぼ半分を中間状態が占め、残りのほぼ半分を変性状態が占めています。
　次に、図10にT0,NIとT0,IUが42℃と47℃、ΔHI（T0,NI）とΔHU（T0,IU）が30 kcal/molと80 kcal/molの場合について熱容量、I状態とU状態の比率、およびΔGIとΔGUの温度依存性を示します。

図10 中間状態から変性状態への転移の早いタンパク質の熱容量曲線（左）と天然状態、中間状態、変性状態の温度依存性（中）、自由エネルギー変化（右）

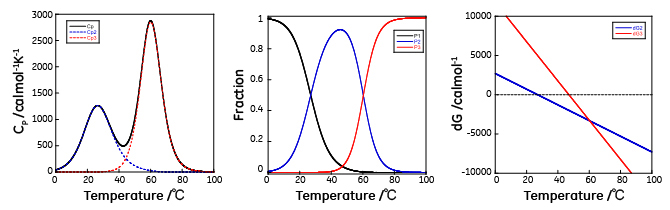
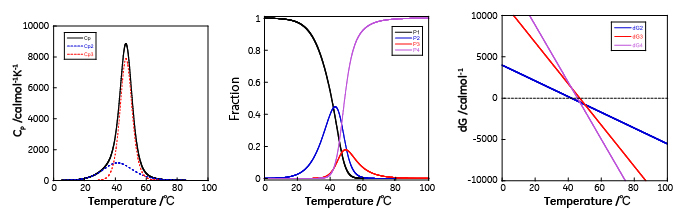
この場合、2つの転移が重なり、熱容量の温度依存性をみると吸熱ピークは1つになっています。47℃以下では中間状態のエネルギーの方が変性状態よりも低いため中間状態の方が多く存在しますが、中間状態と変性状態のエネルギーが40℃から50℃付近で近接するため中間状態の一部は変性状態へと移行し、2つの転移が重なりながら進行することが分かります。このように見かけ上は1つのピークであっても複数の転移が同時に起こっているケースがしばしばあります。従って、DSCにより観測される熱容量から求めたエンタルピー変化（カロリメトリックエンタルピー、ΔHcal）と、各温度での見かけの変性率を用いて2状態転移を仮定して得られるファントホッフエンタルピー（ΔHvan）の比較を行い、2状態転移か多状態転移かどうかを判断することが正しい解析結果を得るために重要です。

モデル5は2種類の中間状態を経て変性するモデルで複数のドメインから構成され、独立に変性が起こる場合に当てはまります。モデル4との違いは中間状態が2種類有り、従って、変性経路も2種類存在することです。

図11 2つのドメインから構成され、2種類の中間状態を経て変性するタンパク質の変性モデル

ΔG4 = ΔG2 + ΔG3

ここで天然状態から中間状態1への転移は転移温度42℃、転移エンタルピーは30 kcal/mol、天然状態から中間状態1への転移は転移温度47℃、転移エンタルピーは50 kcal/molとし、熱容量、各中間状態の比率、および各状態の自由エネルギー差の温度依存性を示しました。なお、簡略化のため変性に伴う熱容量変化（ΔCP）は0としました。

図12 2つのドメインを有するタンパク質の熱容量曲線（左）と天然状態、中間状態、変性状態の温度依存性（中）、自由エネルギー変化（右）

温度の上昇に伴い安定性の低いドメインの変性が始まり、さらに温度の上昇と共に安定性が高いドメインの変性も始まり、それぞれのドメインのみが変性した2種類の中間状態が存在するようになります。また、温度の上昇に伴い、変性していなかったドメインの変性も起こり、完全に変性した状態へ移行します。
なお、各ドメインの安定性が近いために4つの異なる状態が存在するが、片方のドメインがもう片方のドメインよりも大きく安定である場合には、安定性が低いドメインの変性が起こった後に安定性が高いドメインの変性が起こるため、モデル4に従って変性することになります。

 

Reference

1. Brandts, J. F., Hu, C. Q. and Lin, L.-N. Biochemistry 1989, 28, 8588-8596.
2. Freire, E. and Biltonen, R. L. Biopolymers 1978, 17, 463-479.
3. Freire, E. Methods Enzymol. 1994, 240, 502-530.
4. Freire, E., Murphy, K. P., Sanchez-Ruiz, J. M., Galisteo, M. L. and Privalov, P. L. Biochemistry 1992, 31, 250-256.
5. Griko, Y. V., Freire, E., Privalov, G., van Dael, H. and Privalov, P. L. J. Mol. Biol. 1995, 252, 447-459.
6. Hasegawa, J., Uchiyama, S., Tanimoto, Y., Mizutani, M., Igarashi, Y., Sambongi Y. and Kobayashi, Y. J. Biol. Chem. 2000, 275, 37824-37828.
7. Honda, S. Uedaira, H., Vonderviszt, Kidokoro, S and Namba, K. J. Mol. Biol. 1999, 293, 719-732.
8. Iida, T., Nishimura, S., Mochizuki, M, Uchiyama, S., Ohkubo, T., Urade, U., Tanaka, A., and Inui, T. (2008) FEBS J. 275, 233-241.
9. Kidokoro, S. and Wada, A. Biopolymers 1987, 26, 213-229.
10. Privalov P. L. Adv. Protein. Chem. 1979, 33, 167-241
11. Privalov, P. L. and Makhatadze, G. I. J. Mol. Biol. 1992, 224, 715-723.
12. Privalov, P. L. and Makhatadze, G. I. J. Mol. Biol. 1993, 232, 660-79.
13. Privalov G. P. and Privalov P. L. Methods Enzymol. 2000, 323, 31-62
14. Privalov, P. L. and Khechinashvili, N. N. J. Mol. Biol. 1974, 86, 665-84.
15. Sturtevant, J. M. Ann. Rev. Phys. Chem. 1987, 38, 463-488.
16. Uchiyama, S., Hasegawa, J., Tanimoto, Y., Mizutani, M., Igarashi, Y., Sambongi, Y., Kobayashi, Y. Protein Eng. 2002, 15, 455-461.

お問合せフォーム

※日本ポールの他事業部取扱い製品（例: 食品・飲料、半導体、化学/石油/ガス ）はこちらより各事業部へお問い合わせください。